凸优化笔记(1)Why凸优化以及几个基本概念
本文主要参考卡耐基梅隆大学(CMU)的Dr. Ryan Tibshirani教授2017年在Convex Optimization(Course 10-725/36-725)课上(课程网站链接: Convex Optimization)的Lecture Notes。以及参考了现任职牛津大学的Dr. Paul Goulart,以前在ETH任教时Convex Optimization课的 Lecture Notes。如有错误疏漏,烦请指出。如需转载,请联系笔者。
在统计学和机器学习领域,基本上你想做的绝大部分事情都是一种优化问题。所以,面对具体应用的问题,你要做的事情可以概括为如下图所示:

即:如何把头脑中的conceptual idea转换写成寻找决策变量 x 的最优问题 \min_{x\in D} f(x) 。
所以,学习Optimization,就是学习
- 如何把具体问题formulate成为一个优化问题
- 现有算法是如何具体解算上图中的问题 P:\min_{x\in D} f(x)
- 面对不同的具体问题如何选择已有算法或者甚至设计发明适合的算法去解决
绝大部分情况下,你只需要做上述的第1个,就是把问题转换成凸优化问题,并写成标准形式,剩下就交给计算机去解算(利用已有的一些优化工具箱)。第2个和第3个是做前沿研究的人通常要做的事情。
Optimization问题是十分热点的问题,现有算法还有很大的优化提升空间,而且还有很多问题没有得到很好解决,尤其是在Statistics与Machine Learning领域。
Convexity:历史上,优化问题通常聚焦在linear programming(线性规划)。最初人们认为,优化问题是线性还是非线性,是不同的优化问题的根本区别(linear programming的历史请参照华盛顿大学数学系的talks notes: Fast Times in Linear Programming: Early Success, Revolutions, and Mysteries--by Dr. Margaret Wright[墙裂推荐读完]):

而现在人们认为,优化问题是凸还是非凸才是不同的优化问题之间的根本区别。因为有些问题,虽然是非线性,但是好解(因为是凸的),而有些非线性问题,却非常难解(非凸的)。

Convex Set: 集合C是 R^n(n=1,2,3,\cdots) 的子集,如果集合C满足 \forall x, y\in C ,推出 tx+(1-t)y\in C for all0\leq t\leq 1 ,那么集合C就是凸集。
图一中第一行是凸集,第二行是非凸集。
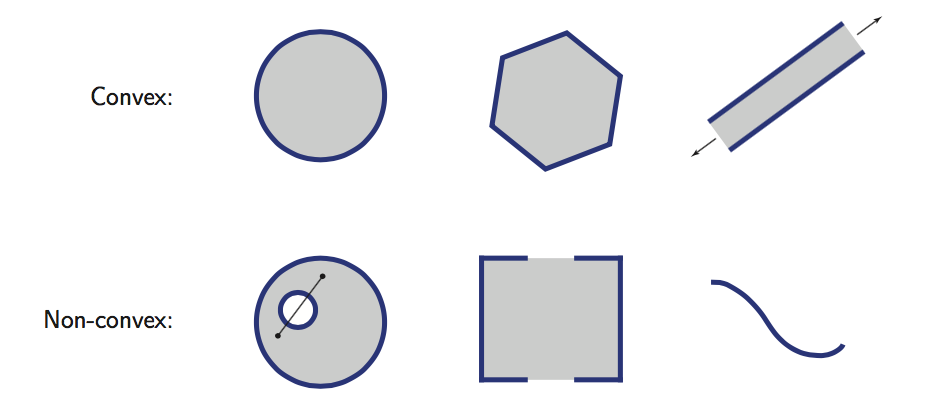
Remark:常见的convex set有hyperplane, halfspace, polytope, polyhedra, ellipsoid, non-negative orthant, norm ball, norm cone, positive (semi)definite matrix等等。凸集之间的某些运算(不是所有运算)依然是凸的。判断一个集合是不是凸集,一般就是两种办法:
- 老老实实check定义中的条件是否满足
- 它是不是某些已知凸集之间的运算,该运算是不是能够保凸。
Convex Function: 如果函数 f: R^n\rightarrow R 满足
- \bold{dom}(f)\subseteq R^n 【 \bold{dom}(f) 是f的定义域】是convex set.
- f(tx+(1-t)y)\leq tf(x)+(1-t)f(y) ,for \forall x, y\in \bold{dom}(f),0\leq t\leq 1

Remark: 除了上述的定义,还有等价地通过epigraph的定义方法:如果 f(x) 的epigraph \{(x,t) : f (x) ≤ t\} 是凸集。或者如果你知道 -f(x) 是concave的,也说明了 f(x) 是convex的。如果 f(x) 一阶可微或者二阶可微,又可以通过一阶或者二阶条件来定义,这里就不细讲了。常见的convex function有 ax+b , e^{ax}, x^a(x>0, a\ge 1或者a\le0), |x|^p(p\ge1), x\log x(x>0), L_p norm( p\ge 1 ), \sum e^{x_i},f(X)=Tr(AX)+b , \sigma_\max (X) 等等。凸函数的某些运算或者变量替换(不是所有运算)依然会是凸的。判断一个函数是不是凸的,一般也是两种办法:
- 老老实实check定义中的条件是否满足
- 它是不是某些已知凸函数之间的运算,该运算是不是能够保凸.
Optimization Problem:

其中 D=\bold{dom}(f)\cap \bigcap_{i=1}^{m}\bold{dom}(g_i)\cap \bigcap_{i=1}^{r}\bold{dom}(h_j) ,也就是所有函数 f, g_i(m个)和h_j(r个) 的交集。 x 称作是决策变量(decision variable),f(x) 称作目标函数(objective function),是个标量; g_i(m个) 称作不等式约束(inequality constraint),是个标量; h_j(r个) 称作等式约束(equality constraint),是个标量。或许有人会问,这里为什么是minimize而不是maximize,其实两个都可以,因为minimize目标函数,等价于maximize目标函数乘以-1。但是呢,人们不想一会儿写成min,一会写成max,弄得看起来乱乱的,就统一形式都写成min。我们面对具体的问题,要做的就是怎么把问题写成如同上式中的形式,并且设计算法寻找 x ,使得 x 在满足那些约束的前提下让objection function最小。如果某个点 x\in D ,也就是 x 在函数 f(x) 的定义域,且把 x 代入到函数 g_i(m个)和h_j(r个) 中分别都满足 g_i(x)\le 0 和 h_j(x)=0 ,那么 x 就称作该优化问题的feasible point(可行解)。feasible point可能压根不存在,也可能存在一个或者多个甚至无穷多个。如果存在多个或者无穷多个feasible point,我们需要找到这些feasible point中,能让 f(x) 最小的那个点 x^{\ast} ,那 x^{\ast} 就是该优化问题的optimal(最优解)。显然这里函数 f, g_i(m个)和h_j(r个) 可以是 x 的任意形式的函数(线性或者非线性),而某些形式会让问题好求解,某些形式会让问题特别难解,甚至至今人们都没有找到解决办法,需要站在前沿的学者们去研究和解决。不等式约束 g_i\le 0 (m个)和等式约束 h_j=0 (r个),根本上说是约束了可行的求解域,如下图所示:

以上定义了什么是优化问题,那么问题来了,什么又是凸优化问题呢?
Convex Optimization Problem: 如果上述优化问题中的函数 f, g_i(m个) 是凸的,而且 h_j(r个) 是affine的,即 h_j(x)=a_j^Tx+b_j, j=1,2,\cdots,r ,那么该问题就是一个凸优化问题。
Remark:
为什么等式约束 h_j 需要是affine的?因为我们在刚才介绍凸集的例图中可以知道,直线是凸集,而曲线是非凸集。affine的等式约束保证了可行域依然是凸集,因为直线->凸集,不是affine的约束那么就是曲线了->非凸集。Convex function有最小值,concave function有最大值。
所以某个问题是凸优化问题,必须满足以下四个条件:
- \bold{dom}(f) 是凸集
- objective function->f(x) 是凸函数
- g_i->m个inequality constraints是convex function
- h_j->r个equality constraints是affine的
我们说了,不等式约束 g_i\le 0 (m个)和等式约束 h_j=0 (r个),根本上说是约束了可行的求解域。那么凸优化问题中: g_i\le 0 导致的可行域是凸的, h_j=0 是affine的,最终的可行域 D=\bold{dom}(f)\bigcap[ \cap_{i=1}^{m}\bold{dom}(g_i\le 0) ]\bigcap[\cap_{i=1}^{r}\bold{dom}(h_j=0)] 就一定是凸的吗?答案是Yes,因为 \bold{dom}(f) 是凸的, \bold{dom}(g_i\le 0) 是凸的因此不等式约束形成的区域的交集 \cap_{i=1}^{m}\bold{dom}(g_i\le 0) 是凸的(凸集的交集一定是凸集,而凸集的并集不一定是凸集), \bold{dom}(h_j=0) 是凸的因此 \cap_{i=1}^{r}\bold{dom}(h_j=0) 是凸的。这三大类约束(定义域+不等式约束区域交集+等式约束区域交集)的交集也是凸集。如下图所示的集合X与Y都是凸集,可以看出他们的交集还是凸集,而他们的并集却不是凸集:
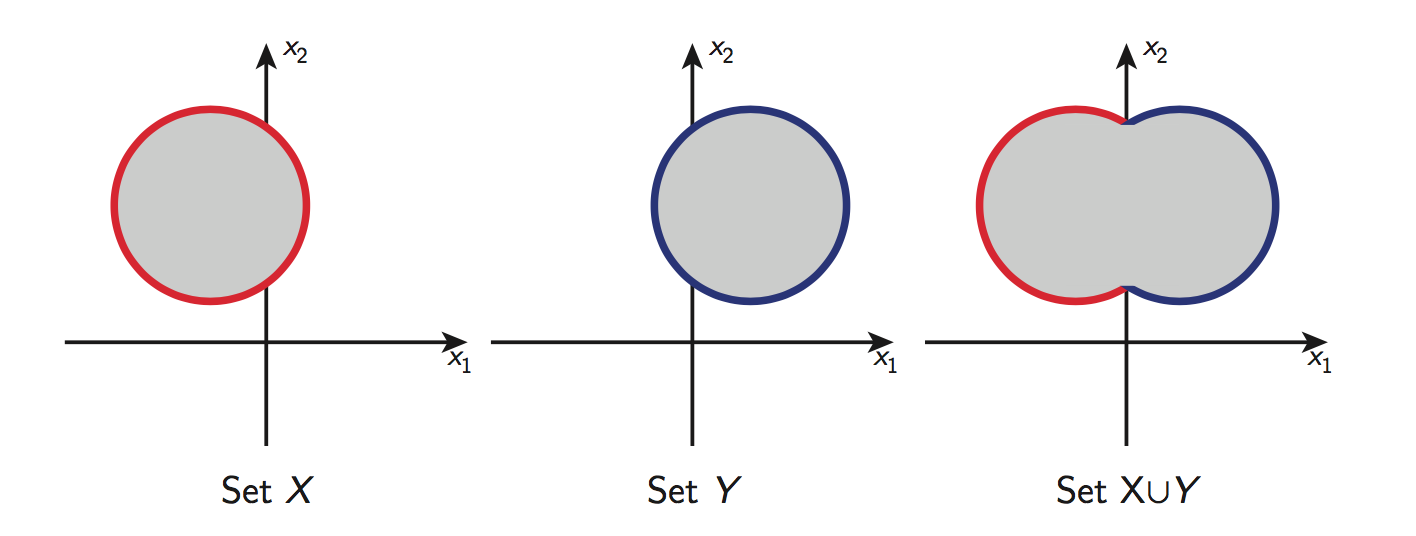
接下来的articles,我们将focus on two dimensions: convex vs. nonconvex(易—>难),and constrained vs. unconstrained(易—>难)。

Convex vs. Non-convex
为什么要研究或者把问题转化为凸优化问题?因为对于凸优化问题,Local minima意味着Global minima。如下图所示,左图是一个凸优化问题,右图是个非凸优化问题:

上图中的左图,因为问题是凸的,所以不管系统的起始点是在图中的红圆圈、蓝圆圈、绿圆圈、黄圆圈还是紫圆圈,只要沿着下降的方向走(你站在某一个点在决定你的下一步怎么走时,下降的方向通常有多个,你可以选取其中任意一个,只要它是下降的),永远都会收敛到同一个最低点,而且这个最低点就是全局最低点。
而上图中的右图,因为问题是非凸的,如果系统起始点在红线和黄线的圆圈处,你沿着下降的方向走,收敛到右图中右边的local minima。而如果系统起始于绿线、蓝线和紫线的圆圈处,沿着下降的方向走,最终收敛到右图中左边的local minima。而这两个local minima不是同一个点。也就是说,你最终的收敛到哪里,依赖于你的系统起始于哪里。而且这两个local minima肯定有一个大,一个小。这是一种非常不好的性质。非凸问题的难点就是面对这种不好的性质,怎么依然找到全局最优解,或者尽量小的那个局部最优解。因为大家都希望不管你起始点在哪里,都能收敛到最小的那个local minima(显然最小的那个local minima就是全局的minima),而不是听天由命,一会儿收敛到较大的那个local minima,一会儿收敛到较小的那个local minima。
Continuous optimization相对于离散化暴力搜索的对比:

文章被以下专栏收录