凸优化算法(1)
本文章将介绍解决凸优化问题中常用到的几种算法,这几种算法都是基于迭代的思想进行求解,以下把这些迭代算法简称为优化算法。此外,还介绍了关于优化算法中解的性质 [1]。
1. 优化迭代算法
首先在介绍优化算法时,把凸优化问题分为了无约束优化问题和有约束优化问题,对应的优化算法也会有所不同,但算法的基本框架都是基于迭代来求解,因此首先介绍算法的基本思想。
1.1 基本思想
优化算法的基本迭代公式:
$$ x^{k+1}=x^{k}+\alpha^kd^k, \tag1 $$
其中
- x^{k+1} 表示第 k+1 时刻得到的解;
- \alpha^k 表示 k 时刻的步长
- d^k 表示 k 时刻的方向
上式可以看出, x^{k+1} 由 x^{k} 、步长和方向决定, x^{k} 是上一步的结果,因此难点在于如何确定合适的步长 \alpha^k ,以及如何确定一个能让函数值下降的方向 d^k 。
例1:下面是函数 f = x^2 + 2y^2 - 4x - 6*y + 9 在(2,3)处所有能使函数下降的方向。为了更加直观地表示某一点处函数下降的所有方向,我们可以在该点处画出一个球体,并在球体表面上标注出使函数下降的方向。
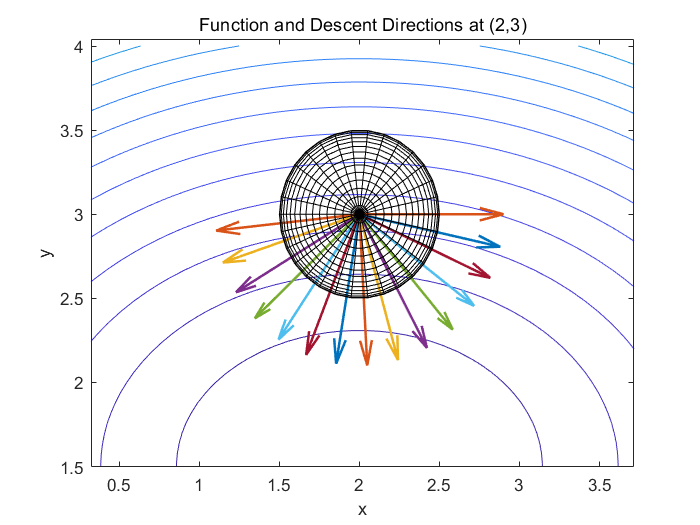
1.2 步长算法
在确定步长的目标是让每一步的 \alpha^k 与 d^k 相乘后使得目标函数尽可能的小,数学表达即为: \alpha^k = \underset{\alpha\ge0}{\text{argmin}} f(x^k+\alpha d^k) \tag2由于 x^k 和 d^k 都已知,因此这是一个一维线性搜索问题。介绍下面两种不精确算法:
- 精确方法:黄金分割法
黄金分割法是一种迭代算法,用于求解一维连续非线性优化问题。它的基本思想是通过对搜索区间进行黄金分割,来逐步缩小搜索范围,从而找到函数的最小值点。具体来说,黄金分割法将搜索区间 [a,b] 分为两个长度相等的子区间 [a,c] 和 [c,b],其中 c = a + 0.618(b-a)。然后,根据函数在子区间的取值情况,选择一个子区间作为新的搜索区间,并重复上述过程,直到达到收敛条件为止。该算法较为简单,再次不再赘述。 - 不精确方法:Amijo Rule
Amijo Rule 是梯度下降法中一种常用的模糊步长搜索方法。其基本思想是从一个大的\alpha开始,在每次迭代中不断减小步长 \alpha^k,直到满足以下不等式:
f(x^k+\alpha^k d^k) \le f(x^k) + \gamma\alpha^k \nabla f(x^k)^Td^k \tag 3 其中,\gamma\in(0,1) 是一个常数,很多时候取值为 0.5(为了后续收敛性证明的需要)。由于在实际应用中,目标函数的形式和梯度的计算方法往往比较复杂,因此 Amijo Rule 可以保证梯度下降法在每次迭代中都能获得一个合适的步长,从而加速收敛。
上述就是迭代算法的基本思想,在介绍如何确定方向之前,我们先考虑此类迭代算法的性能该如何评估?换句话说收敛性如何?为此,下节将介绍函数的一些性质,帮助我们分析算法的收敛性。
2. 优化算法的性质
2.1 函数的强凸性
对于一般的无约束优化问题 \text{min} \, f(x) 且 f(x) 一阶可微,根据KKT条件,最优性条件就为 \nabla f(x)=0 。那自然地会考虑,当 \nabla f(x)\to0 时, x \rightarrow x^* 以及f(x) \rightarrow f(x^*) 他们之间的差距如何刻画?由于迭代算法本质上是一步步去逼近最优解,得到第 k 步的解必然会与最优解存在一点的差距,那么如何来分析第 k 步的解离最优解的距离?此外,如何分析最优值 f(x^*) 离 f(x^{k}) 的距离?其实后者问题,即 ||f(x^{k})-f(x^)||_2^2 更具有实践意义,因为优化本质要找到目标函数的最小值。比如一些实际情况, x 离 x^*还很远,但经过 k 步迭代后得到目标函数值已经非常接近最小值了,并且该值在一定程度下已经可以满足工程实践意义,那么我们就可以让迭代停止了,没必要花更多的时间去逼近最优解。因此,为了能帮助我们更好的刻画这种差距,下面将引入函数的强凸性的概念。
强凸性定义:假设 f(x) 二阶可微,其强凸性有如下定义:
\forall m >0, \forall x \in domf, \nabla^2f(x)\ge mI \tag4
即 \nabla^2f(x)-mI 是半正定矩阵。
如何理解上式?首先给出一个直观的解释:目标函数的强凸性指的是函数的曲率足够强,也就是说,函数图像在任意两点之间的下凸壳都被上方的某个超平面所包含。具体来说,对于一个凸函数 f(x),如果存在一个正实数 \alpha ,使得对于 \forall x, y \in \text{dom}(f) 和 0 \leq \lambda \leq 1,都有:
f(\lambda x + (1-\lambda)y) \le\lambda f(x) + (1-\lambda)f(y) - \frac{m}{2}\lambda(1-\lambda)||x-y||_2^2 \tag5
其中 ||x-y||是 x 和 y 之间的欧几里得距离。这个不等式一阶形式可以表示成:
f(y)≥f(x)+∇f(x)^T(y−x)+ \frac{m}{2}||y−x||^2_2 \tag6
其中 \nabla f(x) 表示 f 在 x 处的梯度。
2.2 分析最优值与第k步函数值的距离
假设函数是强凸的,我们来看看对我们的分析会有什么帮助?比如当 ∇f(x) \to 0 , f(x) 会不会趋于f(x^*) ,或者说还有多少的差距?
(1)分析最优解 f(x^*) 与近似解的距离。
对于 \forall x,只分析式(6)的右边有:
f(x)+∇f(x)^T(y−x)+ \frac{m}{2}||y−x||^2. \tag7
可以看出,式(7)是一个关于 y 的凸函数。自然的想到,如果能求出(7)的最小值,是不是能得到 f(y) 的一个下界?因此,根据凸函数求最小的最优性条件,一阶偏导等于0,首先求驻点方程(对 y 偏导)有:
∇f(x)^T+ m(y-x)=0, \tag8
有 \tilde{y} = x - \frac{∇f(x)}{M} ,上面操作的目的是为了找到使得式(7)值最小的一个 y,把 \tilde{y} 代回(7),可以的得到 f(y) 的下界:
f(y) \ge f(x) - \frac{1}{2m}\begin{Vmatrix}∇f(x)\end{Vmatrix}_2^2. \tag9
目前为止,我们得到一个结论:如果一个函数是强凸的,一定有(8)成立;同时这个式子对于 \forall x 和 \forall y 也是成立的。因此可以把 y 取为目标函数 f 的最优解 y^*,把 f(y^*) 记为 p^*,上式可变为:
p^* \ge f(x)-\frac{1}{2m}\begin{Vmatrix}∇f(x)\end{Vmatrix}_2^2 \tag{10}
对上式做一个移项,又已知对于 \forall x, f(x) 一定有一个下界 p^*,因此有下述不等式成立:
p^* +\frac{1}{2m}\begin{Vmatrix}∇f(x)\end{Vmatrix}_2^2\ge f(x)\ge p^* \tag{11}
由于我们想知道 f(x) 与 p^* 之间的关系,因此再做一次变换有:
\begin{Vmatrix} f(x)-p^* \end{Vmatrix}_2\le \frac{1}{2m}\begin{Vmatrix} ∇f(x) \end{Vmatrix}_2^2 \tag{12}
假设 x=x^k,代入后我们就得到了第 k 步函数值与最优值 p^* 距离的上界。这里解释一下,为什么 f(x)-p^* 需要加一个二范数。首先由于 f(x) 一定大于或等于 p^*,因此 f(x)-p^*一定是大于或等于 0 的,同时 f(x) 与 p^*都是一维的,因此实际上 f(x)-p^*=\begin{Vmatrix} f(x)-p^* \end{Vmatrix}_2 。但二范数实际上表示了欧几里得距离,能更好地表达之前我们所说的最优值和第 k 步函数值之间的差距。
回到最初的问题,当 ∇f(x) \to 0 ,两个解的差距是多少?可以看出,如果知道 f(x) 在 x 处的梯度,虽然我们不能得到一个精确的距离,但知道这个距离一定存在一个上界,就是 \frac{1}{2m}\begin{Vmatrix} ∇f(x) \end{Vmatrix}_2^2 。同时,当 ∇f(x) \to 0 时, f(x) 也就趋近于 f(x^*) 。
2.3 分析当 ∇f(x)\to0 时, x 与 x^* 的距离。
下面证明用到了柯西施瓦茨不等式内积形式: |<a,b>|\le ||a|||b|| ,把 a=-a 代入有: <a,b>\ge -||a|||b|| ,即 <a,b>+||a|||b|| \ge 0 。由柯西-施瓦茨不等式 <a,b>+||a|||b|| \ge 0 ,有:
∇f(x)^T(x^*-x)\ge-\begin{Vmatrix} ∇f(x) \end{Vmatrix}_2\begin{Vmatrix} x^*-x\end{Vmatrix}_2 \tag{13}
首先,假设函数是强凸的,当 y=x^* 时有:
\begin{aligned}f(x) \ge p^* = f(x^*) \ge& f(x) + ∇f(x)^T(x^*-x)+\frac{m}{2}\begin{Vmatrix} x^*-x\end{Vmatrix}^2_2 \\\ge&f(x)-\begin{Vmatrix} ∇f(x) \end{Vmatrix}_2\begin{Vmatrix} x^-x\end{Vmatrix}_2+\frac{m}{2}\begin{Vmatrix} x^*-x\end{Vmatrix}^2_2 \end{aligned} \tag{14}
重新整合上式得到:
\begin{aligned}0\ge&-\begin{Vmatrix} ∇f(x) \end{Vmatrix}_2\begin{Vmatrix} x^*-x\end{Vmatrix}_2+\frac{m}{2}\begin{Vmatrix} x^*-x\end{Vmatrix}^2_2 \end{aligned} \tag{15}
因为 \begin{Vmatrix} x^*-x\end{Vmatrix}_2 \ge 0 ,消去一个后有:
\begin{aligned}\begin{Vmatrix} x^*-x\end{Vmatrix}_2 \le \frac{2}{m}\begin{Vmatrix} ∇f(x)\end{Vmatrix}_2 \end{aligned} \tag{16}
从上述推导可以看出,假设 ∇f(x) 是给定的,如果 m 是一个非常大的数,也就是说该函数是一个非常强凸的函数,可以看到 \frac{1}{2m}\begin{Vmatrix} ∇f(x) \end{Vmatrix}_2^2 , \frac{2}{m}\begin{Vmatrix} ∇f(x)\end{Vmatrix}_2 这两项都非常小,说明非常接近最优解了,也非常接近最优值了。但如果 m 非常小,即使 ∇f(x) \to 0 ,此时的解距离最优解和最优值还有很大差距。通过上述的证明,可以得到两条性质:
(1)对于一个无约束的优化问题的优化算法,基本思路都是让一阶偏导等于0,也相当于在解一个退化后的KKT条件。同时,利用函数的强凸性,我们可以刻画迭代后得到解的精确程度,利用上述结论可以来量化第k步解与最优解的损失程度。
(2)函数的凸性越强,越容易收敛到最低点。
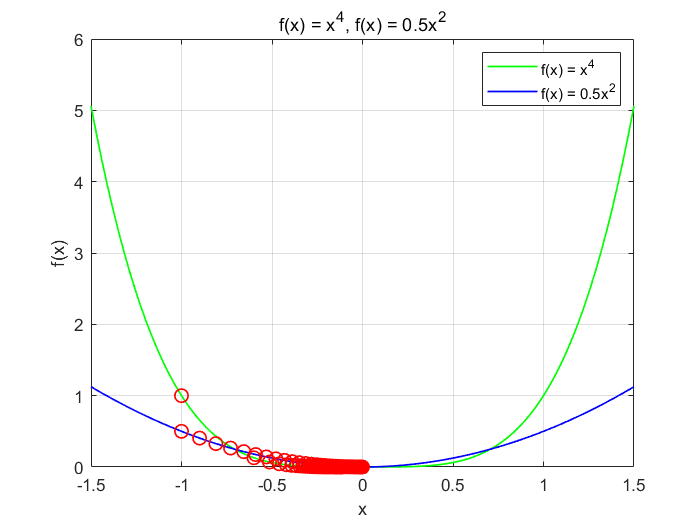
例2:为了能直观的解释函数的强凸性,用两个不同强凸性的函数在梯度下降优化时的表现来说明。
绿色是函数 f_1(x) = x^4 的优化轨迹,蓝色是函数 f_2(x) = 0.5x^2 的优化轨迹。 f_1 比 f_2 的曲率更大,凸性更强。可以看到,两个函数在初始点处的梯度大小是相同的,但是 f_1 函数的优化过程更快,而且更不容易陷入局部最优。
2.3 函数的强凸性上界
假设 f(x) 二阶可微,函数强凸性的上界有如下定义:
\forall M >0, \forall x \in domf, \nabla^2f(x)\le MI ,\tag{17}
即 \nabla^2f(x)-MI 是半负定矩阵。显然,和前面的强凸性相比, m<M。
同样的,另一个等价的定义, \forall x,y \in domf,有
f(y) \le f(x) + ∇f(x)^T(y−x)+ \frac{M}{2}||y−x||^2_2,\tag{18}
对应的有下述性质:
\frac{1}{2M}\begin{Vmatrix} ∇f(x) \end{Vmatrix}_2^2 \le\begin{Vmatrix} f(x)-p^* \end{Vmatrix}_2. \tag{19}通过强凸性上界的定义,给出了最优值与第k步函数值的距离的下界。该性质说明了当 ∇f(x) 很大时, f(x) 距离最优解还很远。
参考
- ^中科大凌青凸优化 https://www.bilibili.com/video/BV1Jt411p7jE/?spm_id_from=333.1007.top_right_bar_window_custom_collection.content.click&vd_source=2a5b81ee6a93316e8a44e68492b11735
文章被以下专栏收录


