电子云的形状原来是这么来的?!
电子云结构是这个世界上最精妙绝伦的结构之一。
总注:只想看科普的读者朋友可以忽视以下所有标注”(可忽视)”的引用块中的内容。
与电子云相关的一个重要的数学知识是---球谐函数。
首先,我们必须要知道,球谐函数从何而来?球谐函数是球坐标系下的 Laplace 方程的解。
Laplace 方程是一个非常重要的偏微分方程,其表达式为:
\bigtriangleup f=0
其中: \bigtriangleup 为 Laplace 算符,是一个标量算符。 f 是一个标量函数。 \bigtriangleup 在不同的坐标系下具有不同的形式,这里我们研究的是其在球坐标系下作用于一个标量函数的解。
(可忽视)
这里我只给出 \bigtriangleup 在直角坐标系和球坐标系下的形式:
直角坐标系下的 Laplace 算符: \bigtriangleup =\frac{\partial^2 }{\partial x^2}+\frac{\partial^2 }{\partial y^2}+\frac{\partial^2 }{\partial z^2}
直角坐标系下的 Laplace 方程: \bigtriangleup f =\frac{\partial^2f }{\partial x^2}+\frac{\partial^2 f}{\partial y^2}+\frac{\partial^2f}{\partial z^2}=0
球坐标系下的 Laplace 算符: \bigtriangleup ={\frac {1}{r ^{2}}}{\frac {\partial }{\partial r }}\left(r ^{2}{\frac {\partial }{\partial r }}\right)+{\frac {1}{r ^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)+{\frac {1}{r ^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \phi ^{2}}}
球坐标系下的 Laplace 方程: \bigtriangleup f ={\frac {1}{r ^{2}}}{\frac {\partial }{\partial r }}\left(r ^{2}{\frac {\partial f }{\partial r }}\right)+{\frac {1}{r ^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial f}{\partial \theta }}\right)+{\frac {1}{r ^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}f}{\partial \phi ^{2}}}=0\left( \bigstar\right)
\left( \bigstar\right) 就是我们要研究的方程。
我们假设标量函数 f 是一个三元函数,即: f=f\left( x,y,z \right) 。在坐标系发生转换时 f 中变量的个数并不会改变。这就意味着, f 从直角坐标系下的表达形式转换到球坐标系下的表达形式之后变量的个数还是三个,即 f=f\left( x,y,z \right)\rightarrow f\left( r,\phi,\theta \right) ,形式变换之后的三个变量分别是: r: 球坐标系径向变量(球的半径), \phi,\theta: 球坐标系下的角变量,其中: \phi 表示经度, \theta 表示维度。
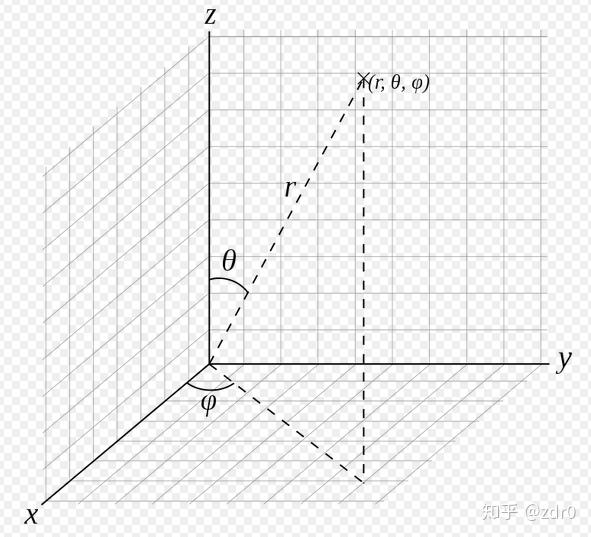
(可忽视)
直角坐标系和球坐标系之间的转换关系式为:
{\displaystyle {r}={\sqrt {x^{2}+y^{2}+z^{2}}}}
{\displaystyle {\theta }=\arccos \left({\frac {z}{r}}\right)=\arcsin \left({\frac {\sqrt {x^{2}+y^{2}}}{r}}\right)=\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)}
{\displaystyle {\phi }=\arccos \left({\frac {x}{r\sin \theta }}\right)=\arcsin \left({\frac {y}{r\sin \theta }}\right)=\arctan \left({\frac {y}{x}}\right)}
现在我们假设 f 在球坐标系下的在三个变量 r,\phi,\theta 上的分量相互独立,这便可以将 f\left( r,\phi,\theta \right) 写成三个一元函数乘积的形式:
f\left ( r,\phi,\theta \right ):=R\left ( r \right )\cdot \Phi\left ( \phi \right )\cdot \Theta\left ( \theta \right )
其中: R\left ( r \right ) 是 f 的径向分量, \Phi\left ( \phi \right ) 是 f 的经度方向分量, \Theta\left ( \theta \right ) 是 f 的纬度方向分量。这个过程有点像因式分解对不对?我们也可以将后面的经度和维度分量合写写在一起,称为角分量(即仅与角有关的分量),并定义为:
Y\left( \phi,\theta \right):=\Phi\left ( \phi \right )\cdot \Theta\left ( \theta \right )
后面我们就会看到,这个二元函数 Y\left( \phi,\theta \right) 就是所谓的球谐函数。定义了 Y\left( \phi,\theta \right) 之后 f 可以写为:
f\left ( r,\phi,\theta \right ):=R\left ( r \right )\cdot Y\left( \phi,\theta \right)
下面我们进入正题:通过球坐标下的 Laplace 方程求解球谐函数 Y\left( \phi,\theta \right) 。(先进行数学推导,最后我们来分析一下得到的解)
(可忽视)
我们利用分离变量法求解球坐标下的 Laplace 方程。首先,我们先做一些准备工作:
f=R\cdot Y\Rightarrow \left\{\begin{matrix} f_{r}=R_{r}\cdot Y\\ f_{\phi }=R\cdot Y_{\phi }\\ f_{\theta }=R\cdot Y_{\theta } \end{matrix}\right.\Rightarrow \left\{\begin{matrix} f_{rr}=R_{rr}\cdot Y\\ f_{\phi\phi }=R\cdot Y_{\phi\phi }\\ f_{\theta\theta }=R\cdot Y_{\theta \theta} \end{matrix}\right.
\Rightarrow\left (r^{2}\cdot f_{r} \right )_{r} =2r\cdot f_{r}+r^{2}\cdot f_{rr}=2r\cdot R_{r}\cdot Y+r^2\cdot R_{rr}\cdot Y
\left (\mathrm{sin}\theta \cdot f_{\theta } \right ) _{\theta}=\mathrm{cos}\theta \cdot f_{\theta } +\mathrm{sin}\theta \cdot f_{\theta\theta } =\mathrm{cos}\theta \cdot R\cdot Y_{\theta }+\mathrm{sin}\theta \cdot R\cdot Y_{\theta \theta }
将上面的结果全部代入球坐标下的 Laplace 方程可得:
\bigtriangleup f ={\frac {1}{r ^{2}}}\left(2r\cdot R_{r}\cdot Y+r^2\cdot R_{rr}\cdot Y\right)+{\frac {1}{r ^{2}\sin \theta }}\left(\mathrm{cos}\theta \cdot R\cdot Y_{\theta }+\mathrm{sin}\theta \cdot R\cdot Y_{\theta \theta }\right)+{\frac {1}{r ^{2}\sin ^{2}\theta }}\cdot R\cdot Y_{\phi\phi }=0
\Rightarrow\left(2r\cdot R_{r}+r^2\cdot R_{rr}\right)\cdot Y=-\left({\frac {\mathrm{cos}\theta}{\sin \theta }} \cdot Y_{\theta }+Y_{\theta \theta }+{\frac {1}{\sin ^{2}\theta }}\cdot Y_{\phi\phi }\right)\cdot R
\Rightarrow\frac{1}{R}\cdot\left(2r\cdot R_{r}+r^2\cdot R_{rr}\right) =-\frac{1}{Y}\cdot\left({\frac {\mathrm{cos}\theta}{\sin \theta }} \cdot Y_{\theta }+Y_{\theta \theta }+{\frac {1}{\sin ^{2}\theta }}\cdot Y_{\phi\phi }\right):=\lambda
从而得到一个二阶常微分方程和一个偏微分方程,分别为:
2r\cdot R_{r}+r^2\cdot R_{rr}-\lambda\cdot R=0\Leftrightarrow2r\cdot \frac{\mathrm{d} R}{\mathrm{d} r}+r^{2}\cdot \frac{\mathrm{d^{2}} R}{\mathrm{d} r^{2}}-\lambda \cdot R=0
{\frac {\mathrm{cos}\theta}{\sin \theta }} \cdot Y_{\theta }+Y_{\theta \theta }+{\frac {1}{\sin ^{2}\theta }}\cdot Y_{\phi\phi }+\lambda\cdot Y=0\left(\bigstar \right)
我们再将 Y\left( \phi,\theta \right):=\Phi\left ( \phi \right )\cdot \Theta\left ( \theta \right ) 代入\left(\bigstar \right) 有:
{\frac {\mathrm{cos}\theta}{\sin \theta }} \cdot\Phi \cdot\Theta_{\theta }+\Phi \cdot\Theta_{\theta\theta }+{\frac {1}{\sin ^{2}\theta }}\cdot \Phi _{\phi\phi }\cdot\Theta+\lambda\cdot \Phi \cdot\Theta=0
\Rightarrow\mathrm{cos}\theta\cdot \sin \theta\cdot\Phi \cdot\Theta_{\theta }+\Phi \cdot\Theta_{\theta\theta }\cdot\sin ^{2}\theta+\Phi _{\phi\phi }\cdot\Theta+\sin ^{2}\theta\cdot \lambda\cdot \Phi \cdot\Theta=0
\Rightarrow\left(\mathrm{cos}\theta\cdot \sin \theta\cdot\Theta_{\theta } +\Theta_{\theta\theta }\cdot\sin ^{2}\theta +\sin ^{2}\theta\cdot \lambda\cdot \Theta\right)\cdot\Phi =-\Phi _{\phi\phi }\cdot\Theta
\Rightarrow\left(\mathrm{cos}\theta\cdot \sin \theta\cdot\Theta_{\theta } +\Theta_{\theta\theta }\cdot\sin ^{2}\theta +\sin ^{2}\theta\cdot \lambda\cdot \Theta\right)\cdot\frac{1}{\Theta} =-\Phi _{\phi\phi }\cdot\frac{1}{\Phi}:=m^2
从而再次得到两个二阶常微分方程:
\mathrm{cos}\theta\cdot \sin \theta\cdot\Theta_{\theta } +\Theta_{\theta\theta }\cdot\sin ^{2}\theta +\sin ^{2}\theta\cdot \lambda\cdot \Theta-m^2\cdot\Theta=0\Leftrightarrow\mathrm{cos}\theta\cdot \sin \theta\cdot\frac{\mathrm{d}\Theta }{\mathrm{d} \theta }+\frac{\mathrm{d^{2}}\Theta }{\mathrm{d} \theta^{2} }\cdot\sin ^{2}\theta +\sin ^{2}\theta\cdot \lambda\cdot \Theta-m^2\cdot\Theta=0
\Phi _{\phi\phi }+m^2\cdot\Phi=0\Leftrightarrow\frac{\mathrm{d^{2}}\Phi }{\mathrm{d} \phi^{2} }+m^2\cdot\Phi=0
现在,我们通过分离变量法得到了三个常微分方程:
\left\{\begin{matrix} 2r\cdot \frac{\mathrm{d} R}{\mathrm{d} r}+r^{2}\cdot \frac{\mathrm{d^{2}} R}{\mathrm{d} r^{2}}-\lambda\cdot R=0\ \ \ \ \ \left( 1 \right)\\ \mathrm{cos}\theta\cdot \sin \theta\cdot\frac{\mathrm{d}\Theta }{\mathrm{d} \theta }+\frac{\mathrm{d^{2}}\Theta }{\mathrm{d} \theta^{2} }\cdot\sin ^{2}\theta +\sin ^{2}\theta\cdot \lambda\cdot \Theta-m^2\cdot\Theta=0\ \ \ \ \ \left( 2 \right)\\ \frac{\mathrm{d^{2}}\Phi }{\mathrm{d} \phi^{2} }+m^2\cdot\Phi=0\ \ \ \ \ \left( 3 \right) \end{matrix}\right.
这三个常微分方程求解的困难程度由低到高分别是: \left(3 \right),\left(1 \right),\left(2 \right) 。
其中有关 \Theta 的方程进行 t=\mathrm{cos}\theta 的变量代换之后 \mathrm{d}t=-\mathrm{sin}\theta\mathrm{d}\theta ,可得到有关 t 的伴随 Legendre 方程,其中 t\in\left[ -1,1 \right] ,该方程需满足在该区间上取有限值,此时必须有: \lambda=l\left( l+1 \right) ,其中 l\in\mathbb{N} 。
这里就不进行求解了,因为求解过程实在是异常复杂。
其实是我不会......(捂脸逃)
最终所求得的球谐函数的表达式为:
Y_{ml}\left ( \theta ,\phi \right ):=\frac{1}{\sqrt{2\pi }}N_{lm}P_{lm}\left ( \cos \theta \right )\exp\left ( im\phi \right )
其中, P_{lm} 称为伴随 Legendre 多项式,其表达式为:
P_{lm}\left( x \right):=\frac{\left (-1 \right )^{m}}{2^{l}\cdot l!}\left ( 1-x^{2} \right )^{\frac{m}{2}}\frac{\mathrm{d} ^{l+m}}{\mathrm{d} x^{l+m}}\left ( x^{2}-1 \right )^{l}
伴随 Legendre 多项式是伴随 Legendre 方程的解。
N_{lm} 称为归一化常数:
N_{lm}:=\sqrt{\frac{2l+1}{2}\cdot \frac{\left ( l-m \right )!}{\left ( l+m \right )!}}
如果把上面的式子都写到一起,就是一个看起来非常可(e)爱(xin)的式子,这个式子就是所谓的球谐函数了,我们来一睹它的尊容:
Y_{ml}\left ( \theta ,\phi \right ):=\frac{1}{\sqrt{2\pi }}\cdot\sqrt{\frac{2l+1}{2}\cdot \frac{\left ( l-m \right )!}{\left ( l+m \right )!}}\cdot\frac{\left (-1 \right )^{m}}{2^{l}\cdot l!}\left ( 1-\cos^{2} \theta \right )^{\frac{m}{2}}\frac{\mathrm{d} ^{l+m}}{\mathrm{d} x^{l+m}}\left (\cos^{2} \theta -1 \right )^{l}\cdot\exp\left ( im\phi \right )
=\frac{1}{\sqrt{2\pi }}\cdot\sqrt{\frac{2l+1}{2}\cdot \frac{\left ( l-m \right )!}{\left ( l+m \right )!}}\cdot\frac{\left (-1 \right )^{m+l}}{2^{l}\cdot l!}\sin^{m}\theta \frac{\mathrm{d} ^{l+m}}{\mathrm{d} x^{l+m}}\sin^{2l} \theta\cdot\exp\left ( im\phi \right )

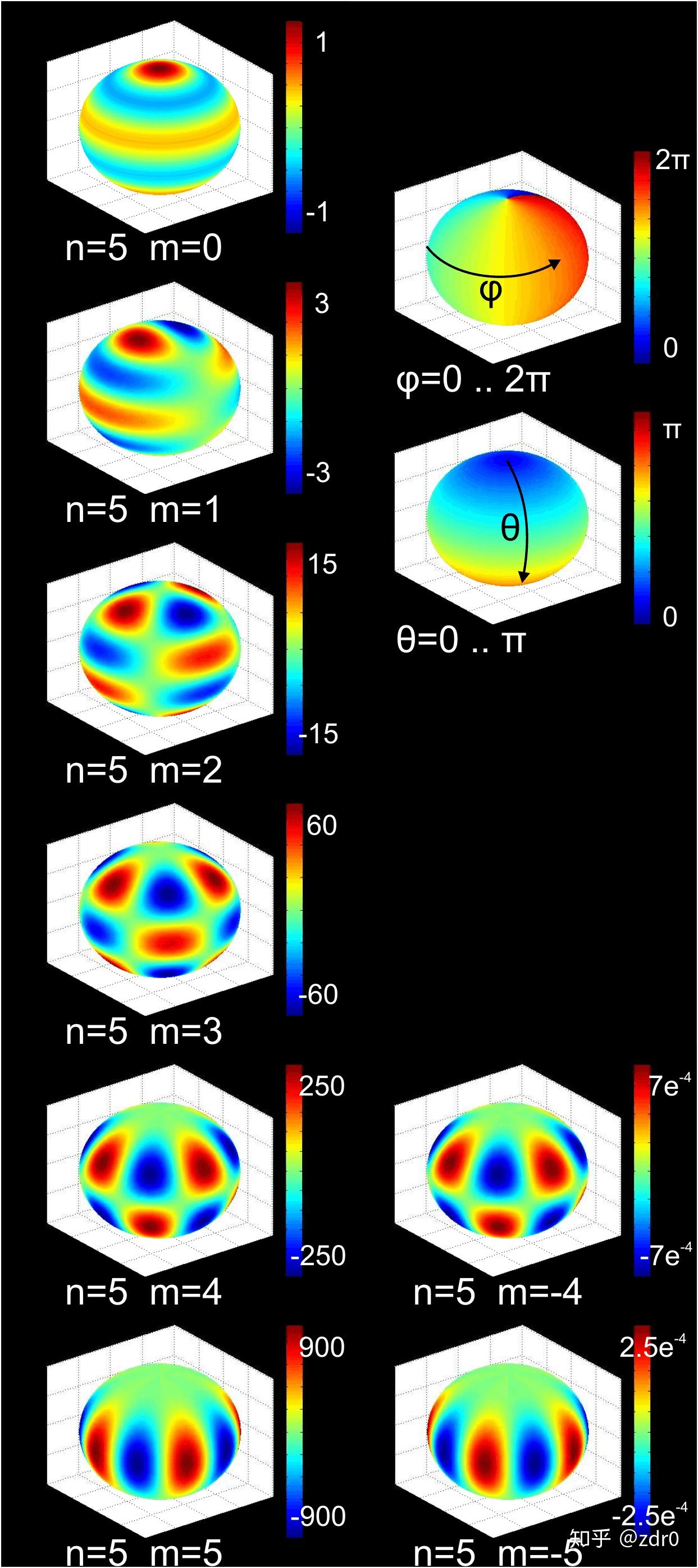
得到球谐函数的表达式之后,我们还应该明确一个问题,就是单粒子球对称位势问题下的薛定谔方程的本征解 \psi\left( r,\phi,\theta \right) 可以描述电子云的形状,该本征解恰好可以被拆成径向分量和角分量的乘积的形式,而其角分量正是球谐函数:
\psi\left( r,\phi,\theta \right):=R_{nl}\left( r \right)\cdot Y_{ml}\left ( \theta ,\phi \right )
下面,我们直接给出单粒子球对称位势问题下的薛定谔方程本征解的径向分量表达式:
R_{nl}=\sqrt{\left ( \frac{2}{na_{0}} \right )^{3}\cdot \frac{\left ( n-l-1 \right )!}{2n \left ( n+l \right )! }}\cdot \left ( \frac{2r}{na_{0}} \right )^{l}\cdot L_{n-l-1}^{2l+1}\left ( \frac{2r}{na_{0}} \right )\cdot \mathrm{exp}\left ( -\frac{r}{na_{0}} \right )
其中: L_{s}^{k} 称为伴随 Laguerre 多项式,其表达式为:
L_{s}^{k}\left ( x \right )=\frac{\mathrm{d}^{s}}{\mathrm{d}x^{s}}\mathrm{exp}\left ( x \right )\frac{\mathrm{d}^{k}}{\mathrm{d}x^{k}}\left ( x^{k}\cdot \mathrm{exp}\left ( -x \right ) \right )
a_0 是 Bohr 半径,其值是: 5.29\cdot10^{-11}\mathrm{m} 。
所以,电子云可以使用以下函数进行描述:
\psi\left( r,\phi,\theta \right)=R_{nl}\left( r \right)\cdot Y_{ml}\left ( \theta ,\phi \right )
其中:
径向本征解(径向波函数):
R_{nl}=\sqrt{\left ( \frac{2}{na_{0}} \right )^{3}\cdot \frac{\left ( n-l-1 \right )!}{2n\left ( n+l \right )! }}\cdot \left ( \frac{2r}{na_{0}} \right )^{l}\cdot L_{n-l-1}^{2l+1}\left ( \frac{2r}{na_{0}} \right )\cdot \mathrm{exp}\left ( -\frac{r}{na_{0}} \right )
L_{s}^{k}\left ( x \right )=\frac{\mathrm{d}^{s}}{\mathrm{d}x^{s}}\mathrm{exp}\left ( x \right )\frac{\mathrm{d}^{k}}{\mathrm{d}x^{k}}\left ( x^{k}\cdot \mathrm{exp}\left ( -x \right ) \right )
角向本征解(球谐函数):
Y_{ml}\left ( \theta ,\phi \right ):=\frac{1}{\sqrt{2\pi }}N_{lm}P_{lm}\left ( \cos \theta \right )\exp\left ( im\phi \right )
P_{lm}\left( x \right):=\frac{\left (-1 \right )^{m}}{2^{l}\cdot l!}\left ( 1-x^{2} \right )^{\frac{m}{2}}\frac{\mathrm{d} ^{l+m}}{\mathrm{d} x^{l+m}}\left ( x^{2}-1 \right )^{l}
N_{lm}:=\sqrt{\frac{2l+1}{2}\cdot \frac{\left ( l-m \right )!}{\left ( l+m \right )!}}
下标 n,l,m 是指三个量子数,分别是主量子数,角量子数和磁量子数,它们的意义分别是:
- 主量子数 n :电子层数,取值为 n=1,2,3,...
- 角量子数 l :轨道量子数(亚电子层数),取值为 l=0,1,2,...,n-1
例如: n=3 ,则 l=0,1,2 ,分别 s,p,d 亚电子层(后面我们会看到相应的分量)
- 磁量子数 m :轨道角动量沿某指定轴的投影,取值为 m=0,\pm1,\pm2,...,\pm l
磁量子数的个数描述了 s,p,d,f,... 亚电子层有多少个分量。
在上面的“部分球谐函数表示”图片中可以很清楚的看到 m 的取值对球谐函数分量个数的影响。
下图是径向波函数在 n,l 取不同值时候的曲线:
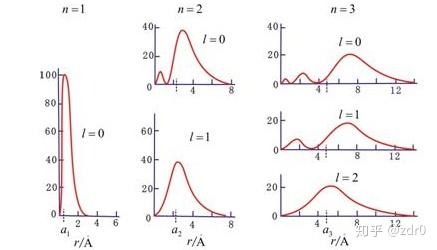
以及瞩目的电子云图形:

我们知道,电子云是径向函数和球谐函数共同作用的结果。究竟是如何作用的呢?我们以 \psi_{300} 为例来进行解释:


其中:
\psi_{300}=R_{30}\cdot Y_{00}=\frac{1}{\sqrt{\pi}}\cdot \left ( \frac{Z}{3a_{0}} \right )^{\frac{3}{2}}\cdot \left ( 1-\frac{2Zr}{3a_{0}}+\frac{2Z^{2}r^{2}}{27a_{0}^{2}} \right )\cdot \exp\left (-\frac{Zr}{3a_{0}} \right )
\psi_{300}=0\Leftrightarrow\frac{1}{\sqrt{\pi}}\cdot \left ( \frac{Z}{3a_{0}} \right )^{\frac{3}{2}}\cdot \left ( 1-\frac{2Zr}{3a_{0}}+\frac{2Z^{2}r^{2}}{27a_{0}^{2}} \right )\cdot \exp\left (-\frac{Zr}{3a_{0}} \right )=0\Leftrightarrow \left ( 1-\frac{2Zr}{3a_{0}}+\frac{2Z^{2}r^{2}}{27a_{0}^{2}} \right )=0
\Rightarrow r=r_{1,2}
显然, r=0 并不是零点。
\psi_{300}\left( 0 \right)=\frac{1}{\sqrt{\pi}}\cdot \left ( \frac{Z}{3a_{0}} \right )^{\frac{3}{2}}
Z 为原子序数。
从上面的 第二图可以看出, \psi_{300} 有两个零点,三个极大值,以及在 r\rightarrow\infty 时, \psi_{300}\rightarrow0 。若我们将极大值处想象成为“最亮的区域”,而零点和趋于零的部分想象成为“最暗的区域”,那么 \psi_{300} 的“亮度变化”是:亮 \rightarrow 暗 \rightarrow 亮 \rightarrow 暗 \rightarrow 亮 \rightarrow 无限趋于暗 。这个变化方式可以从上面的第一图中看出来。
电子云描述的是在电子在空间某处出现的概率大小,上面所说的亮度刻画的就是这个概率。下图是电子云的空间结构:
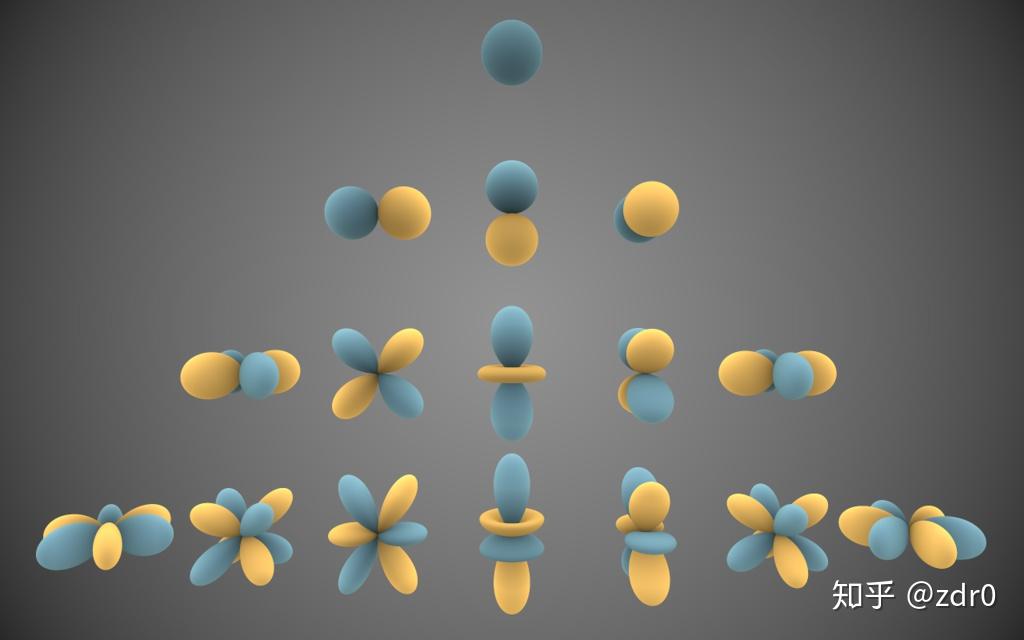
还没关注专栏《数学及自然科学》的朋友请赶快关注吧!您的支持是我最大的动力!
文章被以下专栏收录


